Table of Content
Vectors
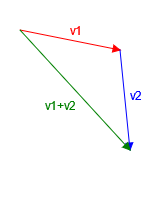
Addition
Vector3 v1 = new Vector3(5,-1);
Vector3 v2 = new Vector3(1,-6);
Vector3 v3 = v1 + v2;
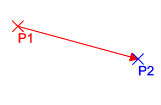
Subtraction
Vector3 pos1 = new Vector3(0,0,0);
Vector3 pos2 = new Vector3(5,-1,0);
Vector3 p1ToP2 = pos2 - pos1;//Points from pos1 towards pos2
Multiplication
Vector3 v1 = createVector(5, 1);
Vector3 longerVector = v1 * 2;//(10, 2)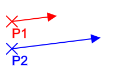
Magnitude
Vector3 v1 = new Vector3(10,20);
float v1Magnitude = v1.magnitude;//length of v1: 22,36Normalization
Vector3 v1 = new Vector3(10,20);
normalizedV1 = v1.normalized;//(0.44, 0.89)

Dot Product
Used for
- Checking if two vectors face in similar direction
- Checking if enemy can see player
- One-Way Trigger/Collider, i.e. Platform that you collide with only from above
v1v2 = 1 when they are facing in the same direction
v1v2 = -1 when they are facing in opposite direction
v1*v2 = 0 when facing 90° right or left of the other direction
Hint: You usually normalize one or both vectors.
Commutative: v1*v2 = v2*v1
v1 * v2 = v1.x * v2.x + v1.y * v2.y
angleV1ToV2 = acos(v1*v2)
Vector3 v1 = new Vector(1,0,0);
Vector3 v2 = new Vector(1,5,0);
float dotProduct = Vector3.Dot(v1, v2);Cross Product
Only useful for 3D-Games.
Used for
- Calculating Normals
- Building structures along slopes
- Shaders
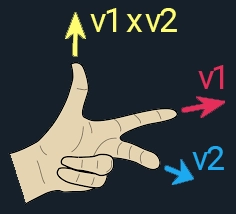
Generates a 3D-vector that is perpendicular to the two given vectors. The length of the resulting vector is equal to the parallelogram which the two input-vectors create.
Anti – Commutative: v1 x v2 = –v2 x v1
Basic Cross Product
Vector3 v1 = new Vector(1,0,0);
Vector3 v2 = new Vector(0,1,0);
float forwardVec = Vector3.Cross(v1, v2);//result: (0,0,1)Coding transform.LookAt yourself with Dot- and Cross Product
Vector3 toTarget = (_lookTarget.position - transform.position).normalized;
Vector3 targetVec = Vector3.forward;
float degrees = Mathf.Acos(Vector3.Dot(myVec, targetVec)) * Mathf.Rad2Deg;
Vector3 rotationAxis = Vector3.Cross(myVec, targetVec); // Axis to rotate by when you want to get a rotation from myVec to targetVec
transform.rotation = Quaternion.AngleAxis(degrees, rotationAxis);Turret-Placement via Cross Product
void Update()
{
Camera cam = Camera.main;//Cache this for better performance!
bool wasHit = Physics.Raycast(cam.transform.position, cam.transform.forward, out RaycastHit hitInfo);
if (wasHit)
{
Vector3 xAxis = Vector3.Cross(Vector3.up, cam.transform.forward).normalized;
Vector3 zAxis = Vector3.Cross(xAxis, Vector3.up).normalized;
_turret.transform.position = hitInfo.point;
_turret.rotation = Quaternion.LookRotation(zAxis, Vector3.up);
}
}By the way, this is the formula for the cross-product, which you really don’t need to memorize:
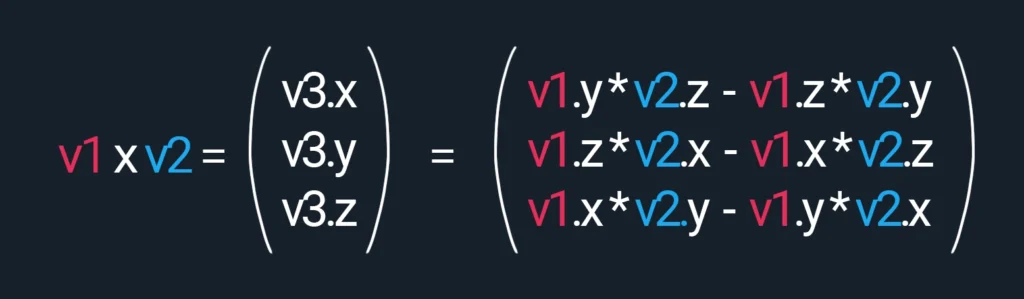
Unity uses a left-handed-coordinate system:
Lerping
Used for animating numbers, vectors, positions, colors
Vector3 startPos = new Vector3(10, 20);
Vector3 endPos = new Vector3(20, 15);
float t = 0.7f;
Vector3 p1 = Vector3.Lerp(startPos, endPos, t);
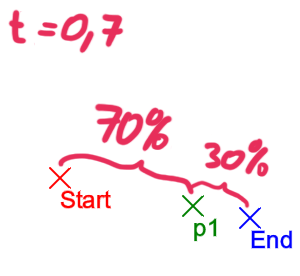
The Lerp-Function “moves” the vector from startPos towards endPos.
The variable t determines how far the rotation has already progressed.
Vector3.Lerp(startPos, endPos, t)
t… value between 0 and 1.
t=0 remains at startPos
t=0.7f travels 70% of the way from startPos towards endPos
t=1 travels to endPos
Basic Lerp
Lerps toward destination, getting slower the closer it gets
float lerpSpeed = 3;
float t = Time.deltaTime * lerpSpeed;
transform.position = Vector3.Lerp(_lerpedTransform.position, mousePosition, t);Lerp over Time
Lerps over fixed duration
-> Animation takes i.e. 8 seconds
-> The further away the destination is the faster it will move towards it.
Warning: When lerping via duration you should never change the origin because it will look weird :).
private float _lerpTimer;
private float _lerpDuration = 8;
void Update()
{
Vector3 origin = Vector3.zero;
Vector3 destination = new Vector3(1, 2, 3);
_lerpTimer += Time.deltaTime;
float t = _lerpTimer / _lerpDuration;
transform.position = Vector3.Lerp(origin, destination, t);
}Movement
Move with constant speed
Move with constant speed towards specific position.
-> Object moves i.e. 3 meters per second
transform.position +=
float moveSpeed = 3;
Vector3 direction = (_target.position - transform.position).normalized;
transform.position += direction * moveSpeed * Time.deltaTime;MoveTowards
Can’t overshoot destination.
Vector3 destination = new Vector3(5,0,0);
Vector3 moveSpeed = 3;
transform.position = Vector3.MoveTowards(transform.position, destination, moveSpeed * Time.deltaTime);Rotations
Set rotation
//Via Angle-Axis
transform.rotation = Quaternion.AngleAxis(45, Vector3.forward);
//Via Euler
transform.rotation = Quaternion.Euler(0, 0, 45);Rotate by degrees
//Rotate around axis (preferred way of rotating)
Vector3 rotationAxis = new Vector3(0, 0, 1);
transform.Rotate(rotationAxis, 180 * Time.deltaTime, Space.World);
//Rotate 180 degrees per Second around the Z-Axis
Vector3 rotationSpeed = new Vector3(0, 0, 180);
transform.Rotate(rotationSpeed * Time.deltaTime, Space.World);
Rotate towards directionvector (instantly)
2D
Vector3 dir = _objToLookAt.transform.position - transform.position;
transform.up = dir;3D
[SerializeField] private Transform _target;
void Update()
{
//rotate towards world-position
transform.LookAt(_target.position);
//Rotate towards direction
Vector3 targetDir = _target.position - transform.position;
transform.rotation = Quaternion.LookRotation(targetDir);
//Let the right side look towards direction
transform.right = targetDir;
}
}Rotate towards directionVector with rotationspeed
2D
//Rotate 90° per second
void Update()
{
Vector3 targetDirection = new Vector3(1,1,0);
transform.up = Vector3.RotateTowards(transform.up, targetDirection, Mathf.Deg2Rad * 90 * Time.deltaTime, 999);
}3D
public Transform _target;
void Update()
{
Vector3 targetDir = _target.position - transform.position;
float degreesPerSecond = 60;
float maxDelta = degreesPerSecond * Time.deltaTime;
transform.rotation = Quaternion.RotateTowards(transform.rotation, Quaternion.LookRotation(targetDir), maxDelta);
}Slerping
Spherical Lerp, used for rotations because lerp looks janky
Lerp vs Slerp
Slerp Rotations
Used for animating rotations.
float t = 0.5;
Quaternion originRotation = Quaternion.identity;
Quaterntion targetRotation =Quaternion.Euler(0, 100, 0);
transform.rotation = Quaternion.Slerp(originRotation , targetRotation, t);The Slerp-Function “rotates” the vector from one rotation towards another.
The variable t determines how far the rotation has already progressed.
t: 0 -> returns Quaternion.identity
t: 1 -> returns targetRotation
t: 0.5 -> returns a Vector that is halfway between origin- and targetRotation (0, 50, 0)
t: 0.75 -> returns a Vector that has rotated 75% from origin- to targetRotation (0, 75, 0)
Basic Slerp
Slerpts toward target-rotation getting slower the closer it gets to the final rotation.
void Update()
{
transform.rotation = Quaternion.Slerp(transform.rotation, Quaternion.Euler(0, -130, 0), Time.deltaTime);
}Slerp over Duration
Performs a rotation over a duration (i.e. 2seconds)
[SerializeField] private float _slerpDuration = 2;
private float _slerpTimer;
void Update()
{
_slerpTimer += Time.deltaTime;
float t = _slerpTimer / _slerpDuration;
transform.rotation = Quaternion.Slerp(Quaternion.identity, Quaternion.Euler(0, -130, 0), t);
}Character Controller
Basic FPS Controller
[SerializeField] private float _moveSpeed = 5;
[SerializeField] private float _lookSensitivity = 5;
[SerializeField] private float _lowerVerticalLimit = -90;
[SerializeField] private float _upperVerticalLimit = 90;
private float _currentXAngle;
private float _currentYAngle;
void Update()
{
//Lookrotation
float horizontalLookInput = Input.GetAxis("Mouse X");
float verticalLookInput = Input.GetAxis("Mouse Y");
_currentYAngle = (_currentYAngle + horizontalLookInput * _lookSensitivity) % 360;
_currentXAngle -= verticalLookInput * _lookSensitivity;
_currentXAngle = Mathf.Clamp(_currentXAngle, _lowerVerticalLimit, _upperVerticalLimit);
transform.rotation = Quaternion.Euler(_currentXAngle, _currentYAngle, 0);
//Movement
float horizontalInput = Input.GetAxis("Horizontal");
float verticalInput = Input.GetAxis("Vertical");
transform.position += (transform.forward * verticalInput + transform.right * horizontalInput) * (_moveSpeed * Time.deltaTime);
}Basic 3rd Person Controller
Hint: For this to work you need the Cinemachine from the Package Manager
//Create a new empty GameObject named FollowTarget and make it a child of the PlayerController.
//Create Cinemachine Virtual Camera and set it to 3rd Person Follow.
//Set FollowTarget the as "follow" of a cinemachine camera.
[SerializeField] private Transform _followTarget;
[SerializeField] private float _moveSpeed = 5;
[SerializeField] private float _lookSensitivity = 3;
[SerializeField] private float _upperVerticalLimit = 45;
[SerializeField] private float _lowerVerticalLimit = 45;
private float _currentXAngle;
private float _currentYAngle;
void Update()
{
//Lookrotation
float horizontalLookInput = Input.GetAxis("Mouse X");
float verticalLookInput = Input.GetAxis("Mouse Y");
_currentYAngle += horizontalLookInput * _lookSensitivity;
_currentXAngle += -verticalLookInput * _lookSensitivity;
_currentXAngle = Mathf.Clamp(_currentXAngle, _lowerVerticalLimit, _upperVerticalLimit);
transform.rotation = Quaternion.Euler(0,_currentYAngle,0);
_followTarget.localEulerAngles = new Vector3(_currentXAngle, 0, 0);
//Movement
float horizontalInput = Input.GetAxis("Horizontal");
float verticalInput = Input.GetAxis("Vertical");
transform.position += (transform.forward * verticalInput + transform.right * horizontalInput) * (_moveSpeed * Time.deltaTime);
}